欧宝体育,欧宝体育app,欧宝娱乐,欧宝体育官网,足球投注平台,电竞下注,注册送彩金,欧宝足球下注,欧宝篮球盘口,欧宝电竞投注,体育投注平台作 P 关于 OA ， OB 的对称点 C ， D ．连接 OC ， OD ．则当 M ， N 是 CD 与 OA ， OB 的交点时，△ PMN 的周长最短，最短的值是 CD 的长．根据对称的性质可以证得：△ COD 是等腰直角三角形，据此即可求解．

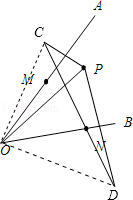
　　【题后思考】本题考查了对称的性质，正确作出图形，理解△ PMN 周长最小的条件是解题的关键．

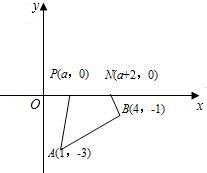
　　【分析】因为 AB ， PN 的长度都是固定的，所以求出 PA + NB 的长度就行了．问题就是 PA + NB 什么时候最短．

　　把 B 点向左平移2个单位到 B ′点；作 B ′关于 x 轴的对称点 B ″，连接 AB ″，交 x 轴于 P ，从而确定 N 点位置，此时 PA + NB 最短．

　　设直线 AB ″的解析式为 y = kx + b ，待定系数法求直线解析式．即可求得 a 的值．

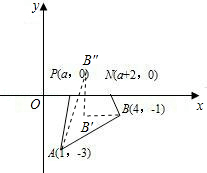
　　【解答】解：将 N 点向左平移2单位与 P 重合，点 B 向左平移2单位到 B ′（2，﹣1），

　　作 B ′关于 x 轴的对称点 B ″，根据作法知点 B ″（2，1），

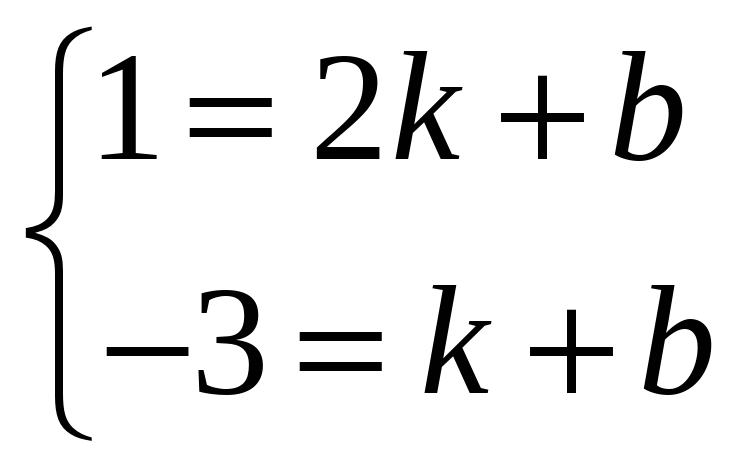
　　3．如图， A 、 B 两点在直线的两侧，点 A 到直线，点 B 到直线， P 为直线上的动点， PA ﹣ PB 的最大值为．

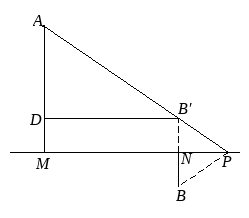
　　【分析】作点 B 于直线 l 的对称点 B ′，则 PB = PB ′因而 PA ﹣ PB = PA ﹣ PB ′，则当 A ， B ′、 P 在一条直线上时， PA ﹣ PB 的值最大．根据平行线分线段定理即可求得 PN 和 PM 的值然后根据勾股定理求得 PA 、 PB ′的值，进而求得 PA ﹣ PB 的最大值．

　　【解答】解：作点 B 于直线 l 的对称点 B ′，连 AB ′并延长交直线 l 于 P ．

　　【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．

　　4．动手操作：在矩形纸片 ABCD 中， AB =3， AD =5．如图所示，折叠纸片，使点 A 落在 BC 边上的 A ′处，折痕为 PQ ，当点 A ′在 BC 边上移动时，折痕的端点 P 、 Q 也随之移动．若限定点 P 、 Q 分别在 AB 、 AD 边上移动，则点 A ′在 BC 边上可移动的最大距离为．

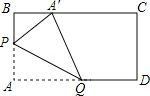
　　【分析】本题关键在于找到两个极端，即 BA ′取最大或最小值时，点 P 或 Q 的位置．经实验不难发现，分别求出点 P 与 B 重合时， BA ′取最大值3和当点 Q 与 D 重合时， BA ′的最小值1．所以可求点 A ′在 BC 边上移动的最大距离为2．

　　当点 Q 与 D 重合时（如图），由勾股定理得 A ′ C =4，此时 BA ′取最小值为1．

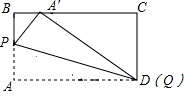
　　【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．

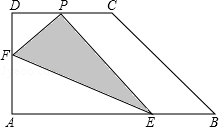
　　【分析】如图，经分析、探究，只有当直径 EF 最大，且点 A 落在 BD 上时， PD 最小；根据勾股定理求出 BD 的长度，问题即可解决．

　　【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．